En cualquier circuito eléctrico, la energía
eléctrica del suministro se entrega a la carga donde se convierte en un trabajo
útil.
Prácticamente, toda la potencia suministrada
no se presentará en la carga debido al efecto de calentamiento y otras
restricciones en la red.
El tamaño de la carga siempre afecta la
cantidad de energía transferida desde la fuente de suministro, es decir,
cualquier cambio en la resistencia de carga resulta en cambios en la transferencia
de potencia a la carga.
El teorema de transferencia de potencia
máxima establece que en una red DC bilateral lineal la potencia máxima se entrega a la carga
cuando la resistencia de carga es igual a la resistencia interna de una fuente.
Prueba del teorema de máxima transferencia de potencia
El teorema de máxima transferencia de
potencia asegura el valor de la resistencia de carga a la que se transfiere la
potencia máxima.
Considere la siguiente red de dos terminales,
a la cual se determina la condición para la potencia máxima, obteniendo la
expresión de potencia absorbida por carga con el uso de malla o métodos de
corriente nodal y luego deriva la expresión resultante con respecto a la
resistencia a la carga RL.
Este es un procedimiento complejo pero la
parte compleja de la red puede reemplazarse con un equivalente de Thevenin.
La corriente a través de la carga es:
La potencia absorbida por la carga es:
La potencia absorbida por la carga es:
Para encontrar el valor de RL,
aplicamos la derivada de PL con respecto a RL y lo
igualamos a cero como sigue:
Por lo tanto, para
transferir la máxima potencia a la carga, la resistencia de carga debe ser
igual a la resistencia equivalente de Thevenin.
Sustituyendo la Rth = RL en la ecuación obtenemos
que la potencia máxima entregada a la carga es:
La figura siguiente muestra una curva de
potencia entregada a la carga con respecto a la resistencia de carga.
Teorema de máxima transferencia de potencia para circuitos AC
Puede afirmarse que la potencia máxima se
transfiere a la carga cuando la impedancia de carga es igual al complejo
conjugado de una impedancia equivalente de una red dada vista desde los
terminales de carga.
Considere el circuito equivalente de Thevenin.
La corriente que fluye a través del circuito es:
Dónde:
Por lo tanto:
La potencia entregada a la carga:
Para la potencia máxima, la derivada de la
ecuación anterior debe ser cero, después de la simplificación obtenemos:
Poniendo la relación anterior en la ecuación
obtenemos:
De nuevo para la máxima transferencia de
potencia, la derivación de la ecuación anterior debe ser igual a cero,
simplificando:
Esto significa que la impedancia de carga
debe ser igual al complejo conjugado de la impedancia equivalente del circuito.
Descarga la separata TEOREMA MÁXIMA TRANSFERENCIA DE POTENCIA aquí.
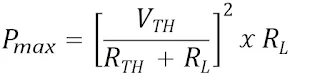
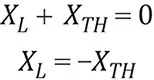
No hay comentarios.:
Publicar un comentario
Gracias por escribirnos. En breve te responderemos.